通過化學氣相沉積法生長的石墨烯中,通常可以觀察到各種構(gòu)型,包括波紋和褶皺。站立的自粘石墨烯褶皺在達到一定高度后會折疊為石墨烯折皺。我們采用連續(xù)近似法來預測由不同金屬基底支撐的石墨烯折皺的形態(tài)。我們的模型基于彈性彎曲和范德華(vdW)相互作用能量的平衡。我們將褶皺的幾何形狀劃分為三個組成部分,并將系統(tǒng)的總能量表示為這三個獨立的能量成分的總和。利用變分法將每個能量分量最小化,并推導出對應部分形狀的參數(shù)解。我們應用6-12 Lennard-Jones勢來模擬石墨烯-基底vdW相互作用的強度。當我們考慮折皺的兩種潛在構(gòu)象時,分析顯示,折疊的雙分子層后面總是跟著一個平坦區(qū)域。該模型還預測了自粘褶皺的臨界高度,結(jié)果與之前的實驗和理論數(shù)據(jù)一致。該模型還預測了自粘褶皺的臨界高度,提供了與先前關于該過渡高度的實驗和理論數(shù)據(jù)一致的結(jié)果。
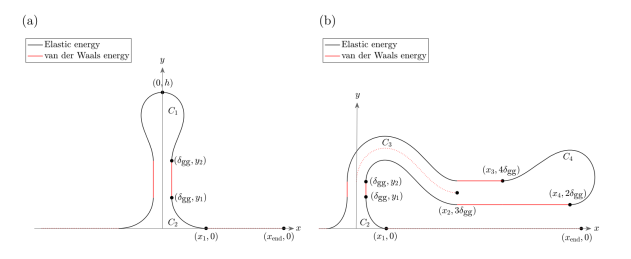
圖1. (a)自粘的石墨烯褶皺和(b)折疊的石墨烯褶皺,支撐在基板上的幾何圖形示意圖。
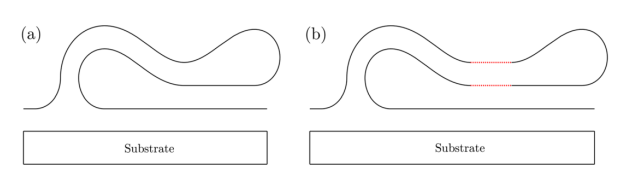
圖2. 折皺的兩種潛在構(gòu)象的結(jié)構(gòu)圖示:(a)構(gòu)象A和(b)構(gòu)象B,與折疊的雙分子層的距離分別為零和非零。
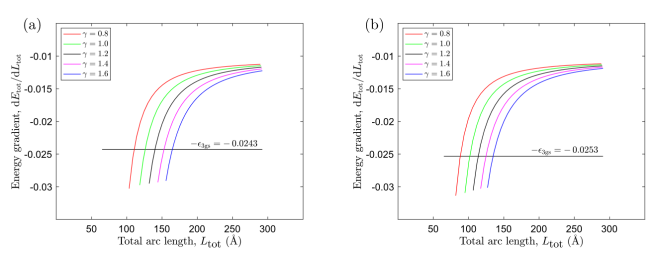
圖3.能量梯度是由(a)Cu(111)基底和(b) Ni(111)基底支撐的折皺的總弧長L
tot的函數(shù)。彩色線表示構(gòu)象A的能量梯度,黑線表示構(gòu)象B的能量梯度,其中交點給出了構(gòu)象A每個γ值的長度L
B。
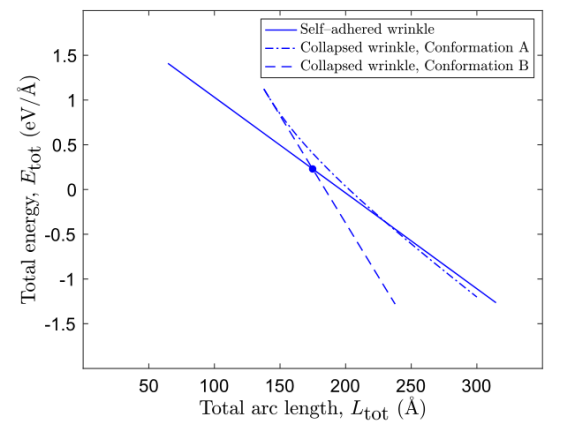
圖4.對于Cu(111)基底支撐的彎曲剛度為γ=1.2 eV的不同褶皺結(jié)構(gòu),總能量E
tot的行為與總弧長L
tot有關。標記點表示臨界長度L
crit,其中自粘褶皺折疊并遵循構(gòu)象B。

圖5. 總能量E
tot的行為與自粘褶皺(實線)和折皺構(gòu)象B(虛線)的總弧長L
tot有關,其中:(a)Cu(111)基底和(b) Ni(111)基底支撐。標記點表示臨界長度L
crit,其中自粘褶皺折疊并遵循構(gòu)象B。
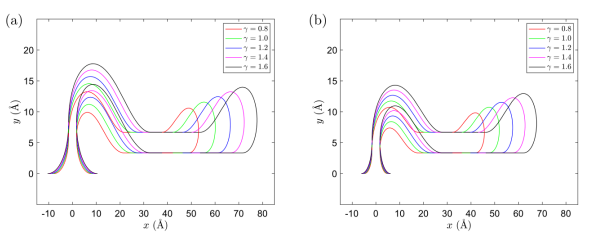
圖6. 在L
tot=L
crit的情況下,不同彎曲剛度的(a)Cu(111)基底和(b) Ni(111)基底上支撐的折皺構(gòu)象。
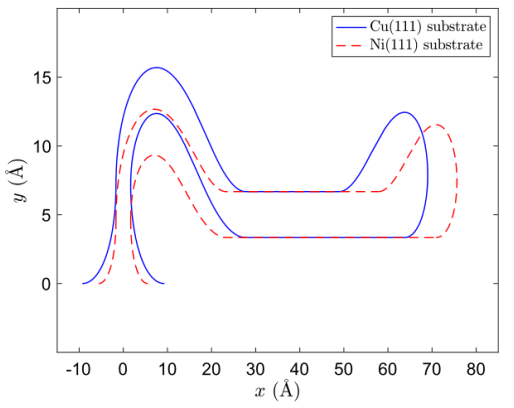
圖7. 固定弧長L
tot=180Å和彎曲剛度γ=1.2 eV的Cu(111)和Ni(111)基底上支撐的折皺構(gòu)象。
相關研究成果由阿卜杜勒阿齊茲國王大學應用學院、阿德萊德大學數(shù)學科學學院的Jabr Aljedani等人于2021年發(fā)表在Applied Physics A (https://doi.org/10.1007/s00339-021-05000-y)上。原文:Variational model for collapsed graphene wrinkles。
轉(zhuǎn)自《石墨烯研究》公眾號
.jpg)








.jpg)


